Ответы на все модули (для контрольного теста) по предмету «Математическая статистика»
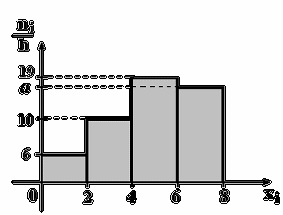
По выборке объема n=100 построена гистограмма частот:
Тогда значение а равно…
15
Формула Стерджесса для определения оптимального числа групп k при группировке данных статистической совокупности имеет вид (N – число единиц в совокупности):
k = 1 + 3,322 ·lg N
Определение искомой характеристики генеральной совокупности внутри какого-то интервала с заданной вероятностью, называется
Интервальной оценкой
Вариант дискретного вариационного ряда, имеющий наибольшую частоту, называется
Модой
Наиболее часто встречающееся значение признака у единиц данной статистической совокупности – это:
Мода
К основным задачам математической статистики относится:
расчет числовых характеристик теоретических распределений вероятностей
В результате измерений некоторой физической величины одним прибором (без систематических ошибок) получены следующие результаты: 10, 13, 13. Тогда несмещенная оценка дисперсии измерений равна
3
Если количественный признак изменяется непрерывно или принимает много значений, то соответствующий вариационный ряд называется
Интервальным
Мода вариационного ряда 2 , 3 , 4 , 8 , 9 , 9 , 10 равна …
9
Если количественный признак принимает дискретные значения, то соответствующий вариационный ряд называется
Дискретным
Медиана вариационного ряда 1 , 2 , 5 , 6 , 7 , 7 , 10 равна …
6
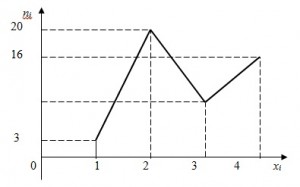
Из генеральной совокупности извлечена выборка объемом n = 49, полигон частот которой имеет вид:
тогда число выборочных значений (число вариант) для xi = 3 равно …
10
По городской телефонной сети было произведено 100 наблюдений и установлено, что средняя продолжительность телефонного разговора составляет 4 минут при среднеквадратичном отклонении 2 мин. Предельная ошибка выборки с вероятностью 0,954 составляет
0,4
В результате 10 опытов получены следующие выборочные значения: 3; 3; 4; 4; 4; 5; 5; 5; 6; 6. Законом распределения для выборки является
|
xi |
3 |
4 |
5 |
6 |
|
pi |
0,2 |
0,3 |
0,3 |
0,2 |
Выборочное наблюдение – это
Несплошное наблюдение
Средним квадратичным отклонением называется
среднее отклонение вариантов от среднего значения
Статистическое распределение выборки имеет вид
|
xi |
-2 |
2 |
3 |
4 |
|
ni |
6 |
4 |
3 |
7 |
Тогда относительная частота варианты x2=2, равна …
0,2
Точечная оценка математического ожидания нормального распределения равна 12. Тогда его интервальная оценка может иметь вид …
(10,6; 13,4)
Для расчета средней арифметической статистической совокупности используется формула (n – объем выборки, xi– выборочные значения):
По формуле для оценки средней величины выборочного распределения (n – объем выборки, xi – выборочные значения) вида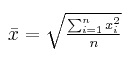 рассчитывается
рассчитывается
Средняя квадратическая
Показателем вариации признака статистической совокупности является
Дисперсия
Характеристикой оценок числовых характеристик по результатам выборочных значений является
несмещенность оценки
Если основная гипотеза имеет вид H0 : p = 0,4, то конкурирующей может быть гипотеза …
H1 : p > 0,4
Гипотеза называется сложной, если …
она частично определяет теоретическое распределение случайной величины по имеющейся выборке ее значений
Если основная гипотеза имеет вид H0 : p = 0,5, то конкурирующей может быть гипотеза …
H1 : p ≠ 0,5
Гипотеза называется простой, если …
если она полностью определяет теоретическое распределение случайной величины по имеющейся выборке ее значений
Уровнем доверия называется вероятность
Если основная гипотеза имеет вид H0 : σ2 = 5, то конкурирующей может быть гипотеза …
H1 : σ2 = 5
Любое предположение о свойствах распределения вероятностей, лежащего в основе наблюдаемых явлений, называется
Статистической гипотезой
Ошибкой второго рода называется вероятность
Если основная гипотеза имеет вид H0 : α = 8, то конкурирующей может быть гипотеза …
H0 : α > 8
Критерии, устанавливающие закон распределения случайной величины, называются …
Критерий согласия
Мощностью критерия называется вероятность
Статистика
имеет распределение, если верна гипотеза
H0 : α1 = α2
Статистика
имеет распределение N(0,1), если верна гипотеза
H0 : p1 = p2
Правило, по которому принимается или отвергается гипотеза, называется …
Критерием
Ошибкой первого рода называется вероятность
Если основная гипотеза имеет вид H0 : α = 18, то конкурирующей может быть гипотеза …
H1 : α ≠ 18
Статистика
имеет распределение Fn1-1, n2-1, если верна гипотеза
H0 : σ12 = σ22
Если основная гипотеза имеет вид H0 : σ2 = 5, то конкурирующей может быть гипотеза …
H1 : σ2 ≠ 5
Величина называется
Эмпирическим корреляционным отношением
Уравнение регрессии вида φ (x; a, b) = abx является
Показательным, Парным
Уравнение регрессии вида φ (x; a, b) = a + bx является
Линейным, Парным
Статистика
где Q1 — межгрупповая сумма квадратов, Q2 — внутригрупповая сумма квадратов, называется
Дисперсионным отношением
Статистический метод, предназначенный для оценки влияния различных факторов на результат эксперимента, называется …
Дисперсионный анализ
Уравнение регрессии φ (x, y; a, b) = a + bx + cy вида является
Множественным, Линейным
Величина
где Q1 — межгрупповая сумма квадратов, Q — полная сумма квадратов, называется
Выборочным коэффициентом детерминации
Основные задачи регрессионного анализа:
Установление формы зависимости некоторой случайной величины от других величин (или одной величины ), т.е. определение вида уравнения регрессии, Оценка функции регрессии и ее параметров
Уравнение регрессии вида
является
Парным, Обратным
По формуле
вычисляются
Парные коэффициенты корреляции
Уравнение регрессии вида φ (x; a, b, c) = a + bx+ cx2 является
Квадратическим, Парным
Величина
называется
Выборочным коэффициентом корреляции
Уравнение регрессии вида
является
Гиперболическим, Парным
Уравнение регрессии вида φ(x; a, b) = axb является
Парным, Степенным
Величина
называется
Внутригрупповая сумма квадратов
Уравнение регрессии вида φ (x; a, b) = aebx является
Парным, Экспоненциальным
Величина
называется
Межгрупповая сумма квадратов
Выявление тесноты связи между переменными и и количественная оценка тесноты этой связи – это основная задача …
Корреляционный анализ
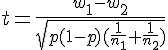
В итоговом тестировании присутствуют измененные вопросы. Вот некоторые из них:
Мода вариационного ряда
5, 8, 8, 9, 10, 11, 13
8
В результате 10 опытов получены следующие выборочные значения: 2; 3; 3; 4; 4; 4; 4; 5; 5; 5. Законом распределения для выборки является
xi 2 3 4 5
pi 0,1 0,2 0,4 0,3
Выявление тесноты связи между переменными X и Y и количественная оценка тесноты этой связи – это основная задача …
Корреляционный анализ