Ответы на 2 модуль по предмету «ИССЛЕДОВАНИЕ ОПЕРАЦИЙ И МЕТОДЫ ОПТИМИЗАЦИИ»
1) Проверить выполнение баланса и привести транспортную задачу к виду, где условие баланса выполнено. Затем решить. Матрица стоимости перевозок имеет вид:
Вектор запасов A =(120,85,75).
Вектор заявок B =(90,70,60,80).
Σ ai<Σ bj, F1=1740, F2 =1740
2) Сформулировать и решить транспортную задачу. Исходный опорный план найти методом минимального элемента. Матрица стоимости перевозок имеет вид:
Вектор запасов A =(40,50,60)
Вектор заявок B =(60,50,40,20,20)
F1=1390, F2=1310
3) Перейти к двойственной и решить задачу
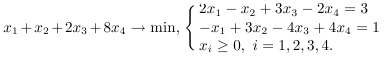
f* = 3
4) Сформулировать и решить транспортную задачу. Исходный опорный план найти методом минимального элемента. Матрица стоимости перевозок имеет вид:
Вектор запасов A =(35,40,40)
Вектор заявок B =(25,25,55)
F1=775, F2=700, F3=660, F4=655
5) Проверить выполнение баланса и привести транспортную задачу к виду, где условие баланса выполнено. Затем решить. Матрица стоимости перевозок имеет вид:
Вектор запасов A =(45,35,70,60).
Вектор заявок B =(40,35,55,60).
Σ ai >=Σ bj , F1=1130(1490?), F2 =795
6) Фабрика производит два лака — для внутренних и наружных работ. Для производства лаков используется два исходных продукта — нефть и кислота. Максимально возможные суточные запасы для этих продуктов определяются емкостями их хранения и равны 6 и 8 тонн (т), соответственно. Для производства 1 т лака для внутренних работ расходуется 1 т нефти и 2 т кислоты, а для производства 1 т лака для наружных работ расходуется 2 т нефти и 1 т кислоты. Суточный спрос на лак для наружных работ не превышает 2 т. Спрос на лак для внутренних работ неограничен.
Доход от реализации 1 т лака для внутренних работ равен 3 млн рублей, а доход от реализации 1 т лака для наружных работ — 2 млн рублей.
Необходимо определить, какое количество лака каждого вида должна производить фабрика в сутки, чтобы доход от его реализации был максимальным.
3×1 + 2×2→ max, x1 + 2×2≤ 6, 2×1+x2 ≤ 8, x2≤ 2, x1 ≥ 0, x2≥ 0
7) Фирма Лявон производит 2 типа деревянных игрушек: крестьяне (КР) и коровы (КО). КР продается за 27$ и требует материалов стоимости 10 $ и нематериальных расходов на сумму 14 $. КО стоит 21 $, требует материалов на 9 $ и нематериальных расходов в размере 10 $.
Производство игрушек включает 2 типа работ: резьбу и окраску. КР требует 1 час резьбы и 2 часа окраски. КО требует 1 час резьбы и 1 час окраски.
Каждую неделю Лявон получает все необходимые расходные материалы, но может использовать не более 80 часов для резьбы и не более 100 часов для окраски. Заказы на КР не превосходят 40 в неделю, а заказы на КО неограничены. Лявон желает максимизировать недельный доход (стоимость проданных игрушек минус расходы). Построить математическую модель и решить (x1 — КР, x2 — КО, z — целевая функция).
x*1 =20, x*2 =60, z* = 180 $
8) Решить графически задачу линейного программирования вида
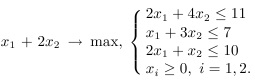
f* = 5/2+3
9) Решить графически задачу линейного программирования вида
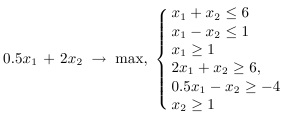
f* = 10