Ответы на 1 модуль по предмету «Математическая статистика»

Ответы на 1 модуль по предмету «Математическая статистика»

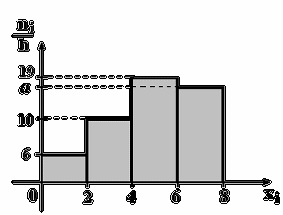
По выборке объема n=100 построена гистограмма частот:

Тогда значение а равно…

15

Формула Стерджесса для определения оптимального числа групп k при группировке данных статистической совокупности имеет вид (N – число единиц в совокупности):

k = 1 + 3,322 ·lg N

Определение искомой характеристики генеральной совокупности внутри какого-то интервала с заданной вероятностью, называется

Интервальной оценкой

Вариант дискретного вариационного ряда, имеющий наибольшую частоту, называется

Модой

Наиболее часто встречающееся значение признака у единиц данной статистической совокупности – это:

Мода

К основным задачам математической статистики относится:

расчет числовых характеристик теоретических распределений вероятностей

В результате измерений некоторой физической величины одним прибором (без систематических ошибок) получены следующие результаты: 10, 13, 13. Тогда несмещенная оценка дисперсии измерений равна

3

Если количественный признак изменяется непрерывно или принимает много значений, то соответствующий вариационный ряд называется

Интервальным

Мода вариационного ряда 2 , 3 , 4 , 8 , 9 , 9 , 10 равна …

9

Если количественный признак принимает дискретные значения, то соответствующий вариационный ряд называется

Дискретным

Медиана вариационного ряда 1 , 2 , 5 , 6 , 7 , 7 , 10 равна …

6

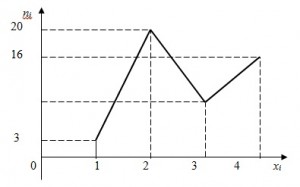
Из генеральной совокупности извлечена выборка объемом n = 49, полигон частот которой имеет вид:

тогда число выборочных значений (число вариант) для x_i = 3 равно …

10

По городской телефонной сети было произведено 100 наблюдений и установлено, что средняя продолжительность телефонного разговора составляет 4 минут при среднеквадратичном отклонении 2 мин. Предельная ошибка выборки с вероятностью 0,954 составляет

0,4

В результате 10 опытов получены следующие выборочные значения: 3; 3; 4; 4; 4; 5; 5; 5; 6; 6. Законом распределения для выборки является

xi	3	4	5	6
pi	0,2	0,3	0,3	0,2

Выборочное наблюдение – это

Несплошное наблюдение

Средним квадратичным отклонением называется

среднее отклонение вариантов от среднего значения

Статистическое распределение выборки имеет вид

xi	-2	2	3	4
ni	6	4	3	7

Тогда относительная частота варианты x₂=2, равна …

0,2

Точечная оценка математического ожидания нормального распределения равна 12. Тогда его интервальная оценка может иметь вид …

(10,6; 13,4)

Для расчета средней арифметической статистической совокупности используется формула (n – объем выборки, x_i– выборочные значения):

По формуле для оценки средней величины выборочного распределения (n – объем выборки, x_i – выборочные значения) вида 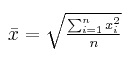  рассчитывается

Средняя квадратическая

Показателем вариации признака статистической совокупности является

Дисперсия

Характеристикой оценок числовых характеристик по результатам выборочных значений является

несмещенность оценки